Il Liber abbaci, più noto come Liber abaci, è un testo medievale in latino di argomento matematico. Scritto nel 1202 dal pisano Leonardo Fibonacci, che lo riscrisse nel 1228 è ritenuto uno dei più importanti libri di matematica del Medioevo. Il Liber abaci è un ponderoso trattato di aritmetica e algebra con il quale, all'inizio del XIII secolo, Fibonacci ha introdotto in Europa il sistema numerico decimale indo-arabico e i principali metodi di calcolo ad esso relativi. In effetti il libro non tratta l'utilizzo dell'abaco e il suo titolo può essere tradotto in Libro del calcolo. In effetti alcuni credono che il titolo sia sbagliato, dato che abaco per i greci, i romani e i maestri d'abaco dei secoli precedenti era uno strumento di calcolo. Fibonacci invece riserva questa denominazione all’aritmetica-algebra applicativa in genere. Su questo testo, per oltre tre secoli, si formeranno maestri e allievi della scuola toscana. L’equilibrio fra teoria e pratica era pienamente raggiunto. Fibonacci dice:
"Ho dimostrato con prove certe quasi tutto quello che ho trattato"
Quando il Liber Abaci fu scritto, in Europa la matematica era praticamente inesistente, se si escludono le traduzioni dei testi classici (gli Elementi di Euclide, per esempio) ma che comunque era ancora molto poco diffusi. Anche rispetto ai suoi maestri arabi Fibonacci compie un’opera unica se non per originalità per mole.
La prima edizione moderna del Liber abaci è stata curata da Baldassarre Boncompagni Ludovisi nel 1857 sul manoscritto del 1228, in quanto quello del 1202 è andato perduto. È un’opera che non ha precedenti in Europa e sfida quelle esistenti nel mondo islamico e classico, è evidente comunque che Fibonacci trae molto dalle opere di matematici arabi quali al-Khwarizm e Abu Kamil. È l’opera più nota e importante di Fibonacci, enorme (459 pagine nell’edizione in-quarto del Boncompagni), composta in 15 capitoli:
- La conoscenza delle nove figure indiane, e come con esse si scrivano tutti numeri; quali numeri si possano tenere in mano e come, e l’introduzione all’abaco.
- La moltiplicazione degli interi.
- L’addizione degli stessi.
- La sottrazione dei numeri minori dai maggiori.
- La divisione dei numeri interi per numeri interi.
- La moltiplicazione degli interi con le frazioni, e delle frazioni senza interi.
- La somma, la sottrazione e la divisione degli interi con le frazioni e la riduzione delle parti di numeri in parti singole.
- L’acquisto e la vendita delle merci e simili.
- I baratti delle merci, l’acquisto di monete e simili.
- Le società fatte tra consoci.
- La fusione delle monete e regole correlative.
- La soluzione di questioni diverse, dette miscellanee.
- La regola delle doppia falsa posizione, e come con essa si risolvano pressoché tutte le questioni miscellanee.
- Il calcolo delle radici quadrate e cubiche per moltiplicazione e divisione o da estrazione e il trattato dei binomi recisi e delle loro radici.
- Le regole delle proporzioni geometriche; e le questioni di algebra e almucabala.
L’opera è suddivisa in quattro parti, la prima (che comprende i primi sette capitoli) è un’introduzione all’algebra e ai nuovi numeri, non fa riferimenti alla vita reale ma presenta esempi sempre più complessi così da abituare il lettore ai nuovi numeri. Seguono poi quattro capitoli che presentano molti possibili problemi nella mercatura, qui il lettore mette alla prova le nuove conoscenze e capisce la superiorità dell’algoritmo indiano rispetto a quello romano. Il dodicesimo capitolo è il più ampio, comprende problemi di matematica “divertente”, uomini che trovano borse, conigli che si moltiplicano, divisione di cavalli, ecc. La terza parte (tredicesimo capitolo) tratta il metodo della doppia falsa posizione, uno dei metodi più potenti della matematica araba e medioevale. L’ultima parte tratta questioni più astratte, estrazione di radici, binomi recisi e proporzioni con la geometria. Vengono presentate le novem figure degli indiani e il signum 0, operazioni su interi e le frazioni, criteri di divisibilità, ricerca del massimo comun divisore e il minimo comune multiplo, regole di acquisto e di vendita, cambi monetari, regole del tre semplice e tre composto, ecc. La parte algebrica è dedicata interamente allo studio delle equazioni algebriche quadratiche secondo i metodi di al-Khwarizm, Abu Kamil, Al-Karaji. Definisce solo tre termini primitivi dell’algebra, il termine noto (numerus), la radice quadrata (radix o cosa), il quadrato (census), che gli serviranno poi per studiare le equazioni dei primi due gradi tratte dall’algebra di al-Khwarizm, che introduce tramite queste sei equazioni:
Studierà anche binomi e trinomi associati alle equazioni, l’algoritmo risolutivo e la sua relativa giustificazione geometrica e una novantina di problemi risolvibili con le conoscenze apprese nel libro. I nuovi algoritmi presentati da Fibonacci, erano per l'epoca, procedure di calcolo scritte in linguaggio colloquiale che intendevano facilitare la risoluzione dei problemi di calcolo evitando l'utilizzo dell'abaco, fino ad allora sostanzialmente indispensabile, dato che si operava con il sistema numerico romano. La maggior parte dei metodi aveva inoltre fondamento teorico nel metodo principale delle Proporzioni e negli altri algoritmi presentati negli Elementi di Euclide. Tra i problemi trattati 22 sono tratti da Al-Khwarizim e 53 da Abu Kamil; si può quindi dire che l’algebra di Fibonacci non è altro che una raccolta riassuntiva di quella di Al-Khwarizim e Abu Kamil. I quindici capitoli del libro sono colmi di problemi di natura disparata ma il dodicesimo (“De Regulis Erractis”) è quello più ricco e vario, dove tratta i numeri perfetti e il problema della coppia di conigli, quello per cui è famoso: “Determinare quanti conigli si avranno alla fine dell’anno partendo da una coppia che sarà fertile a partire dal secondo mese.”
Fonte: Wikipedia

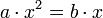
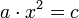

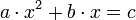
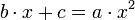
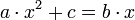














0 commenti:
Posta un commento